Теория n-мерных пространств: от Евклида до современной науки
Исторические корни
Первые шаги в изучении многомерных пространств были сделаны древнегреческими математиками, такими как Евклид и Пифагор. Евклид, в частности, разработал аксиомы и теоремы, касающиеся геометрии двух- и трехмерных пространств. Его работа «Начала» (около 300 г. до н.э.) стала фундаментом для дальнейших исследований в области геометрии.

Однако понятие пространств, имеющих более трех измерений, долгое время оставалось за пределами научного интереса. Лишь в XIX веке немецкий математик Георг Бернхард Риман предложил концепцию многомерных пространств в своей работе «О гипотезах, лежащих в основании геометрии» (1854). Риман ввел понятие «многомерного многообразия», что позволило математикам рассматривать пространства с любым числом измерений.
Основные концепции
Векторные пространства
Одним из ключевых понятий в теории n-мерных пространств является векторное пространство. Векторное пространство — это множество векторов, для которых определены операции сложения и умножения на число, удовлетворяющие определенным аксиомам. Размерность векторного пространства определяется числом линейно независимых векторов, образующих базис этого пространства.
Многомерные многообразия
Многомерное многообразие — это обобщение понятия поверхности на произвольное число измерений. Оно локально подобно евклидовому пространству, но может обладать более сложной глобальной структурой. Примером многомерного многообразия является n-мерная сфера, определяемая как множество точек в (n+1)-мерном евклидовом пространстве, находящихся на фиксированном расстоянии от заданной точки.
Метрики и расстояния
Важным аспектом теории n-мерных пространств является введение метрик, которые позволяют определять расстояния между точками. Метрика — это функция, удовлетворяющая аксиомам неотрицательности, симметрии и неравенству треугольника. В случае евклидова пространства метрика определяется как стандартное расстояние между точками.
Современные приложения
Теория относительности
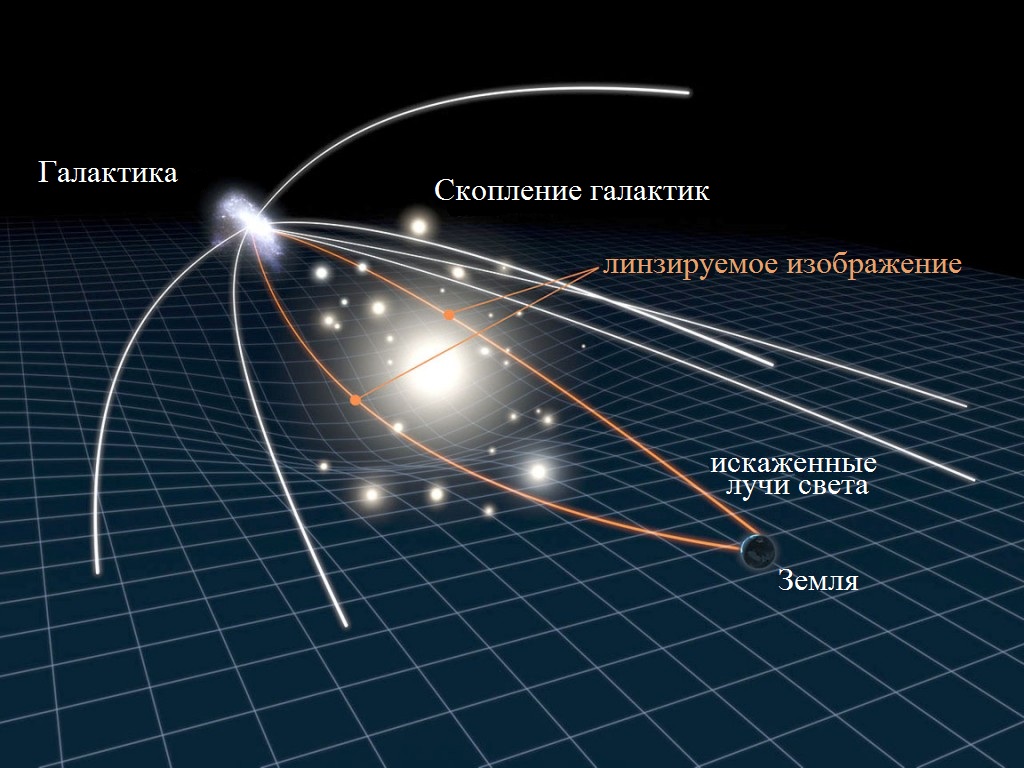
Одним из наиболее известных применений многомерных пространств является общая теория относительности, разработанная Альбертом Эйнштейном. В этой теории пространство-время рассматривается как четырехмерное многообразие, где три измерения представляют пространство, а четвертое — время. Геометрия этого многообразия определяется метрикой, зависящей от распределения массы и энергии.
Квантовая механика
В квантовой механике состояния системы описываются волновыми функциями, которые являются элементами гильбертова пространства — бесконечномерного векторного пространства. Эти пространства позволяют описывать сложные квантовые системы и их эволюцию во времени.
Математическая физика и теория струн
Теория струн — одно из наиболее перспективных направлений современной теоретической физики, также опирается на концепцию многомерных пространств. В этой теории элементарные частицы рассматриваются как одномерные «струны», вибрации которых происходят в пространстве с большим числом измерений. Число измерений в теории струн может достигать 10 или 11, в зависимости от конкретной модели.
Заключение
Теория n-мерных пространств представляет собой мощный инструмент для исследования и понимания сложных систем в математике и физике. От древнегреческой геометрии до современных теорий относительности и струн, эта концепция продолжает играть ключевую роль в развитии науки. Благодаря многомерным пространствам мы можем более глубоко понять природу пространства и времени, а также взаимодействие элементарных частиц.

